制約をもつ組合せ最適化問題を量子計算機で高精度に解くための手法を開発

〜量子ソフトウェアの要素技術への応用に期待〜

2024年3月14日
早稲田大学

制約をもつ組合せ最適化問題を量子計算機で高精度に解くための手法を開発
〜量子ソフトウェアの要素技術への応用に期待〜

発表のポイント
〇現実世界の組合せ最適化問題は一般的に多くの制約（守らなければならないルール）を含むため、制約を効率的に取り扱う量子アルゴリズムの開発は重要である。
〇本研究では、組合せ最適化問題がもつ制約を取り扱うための制約適合処理手法を構築し、変分法を用いた量子アルゴリズムと組み合わせることで、量子計算機の精度を改善する手法を開発した。
〇本手法を取り込んだ量子計算機ソフトウェアの開発により、高精度に現実世界の組合せ最適化問題を解くことが期待できる。

量子アニーリング計算機※1やゲート型量子計算機※2といった量子計算機を現実世界の組合せ最適化問題※3に活用するためには、組合せ最適化問題がもつ制約を効率的に取り扱うことが重要となります。これを受け、早稲田大学理工学術院講師の白井達彦（しらいたつひこ）氏、同大学理工学術院教授の戸川望（とがわのぞむ）氏らの研究グループは、制約をもつ組合せ最適化問題を量子計算機で精度高く解くための新しい手法（図１）を開発しました。さらに、本研究グループは、この手法を量子アニーリング計算機およびゲート型量子計算機に適用し、実量子計算機でその有効性を確認しました。

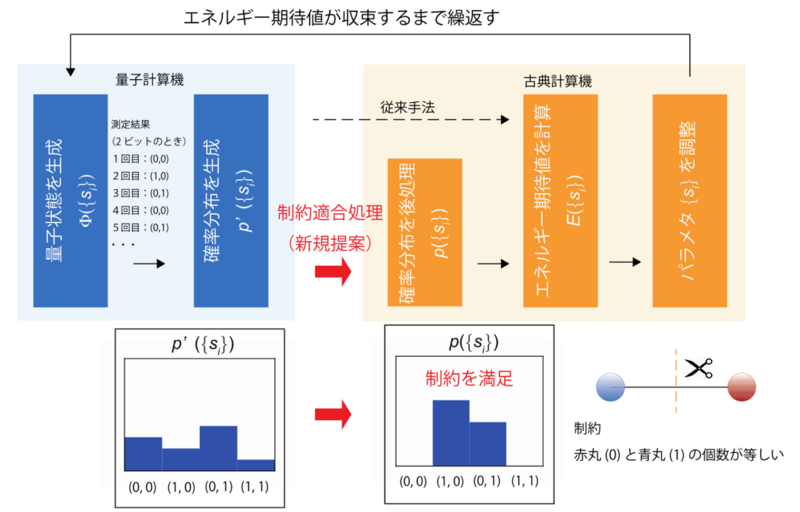
図1. 提案手法の概要
（グラフ分割問題※4（２頂点）を例に）量子計算機から出力される解を、制約を満たす解に変換する制約適合処理手法を組み込んだ量子アルゴリズム

本研究成果は、米国のIEEE Computer Societyが発行する『IEEE Transactions on Quantum Engineering』online版にEarly Access Articlesとして2024年mm月dd日（）（現地時間）に掲載されました。
論文名：Post-processing variationally scheduled quantum algorithm for constrained combinatorial optimization problems

（１）これまでの研究で分かっていたこと（科学史的・歴史的な背景など）
現実世界のあらゆるところに存在する組合せ最適化問題は大規模になるほど、従来型のコンピュータで最適解を得ることが困難になるため、様々な解法が研究されています。中でも近年、量子アニーリング計算機やゲート型量子計算機といった量子力学の原理に従って動作する新しいタイプの計算機が注目されています。量子計算機は国内外で研究開発され、一般のユーザーもクラウド上で使用できる段階になっています。

しかし、量子計算機を活用するにはまだ課題が多くあります。とくに、現在の量子計算機はノイズの影響があるため、エラーなく実行できる時間が制限されます。そのため、短時間で計算することができる量子アルゴリズムの開発が重要となります。ノイズがある量子計算機が短時間の計算処理によって組合せ最適化問題を解法する手法として、これまで変分法※5を用いた量子アルゴリズムが開発されてきました。しかし、後述する制約をもつ組合せ最適化問題では、十分な精度を達成することは難しいという問題がありました。

（２）今回の新たに実現しようとしたこと、明らかになったこと
今回の研究では、制約を満たさない解に対し、制約を満たす解に変換する制約適合処理手法を構築し、変分法と組み合わせることで、制約をもつ組合せ最適化問題を解くための量子アルゴリズムを構築しようと試みました。

たとえば、図1では、２個の頂点をもつグラフを１個の頂点をもつ2個のグラフに分割する問題を考えます。各頂点について1個の量子ビットを対応させます。すると２個の量子ビットが必要となります。２個の量子ビットのうち、一方は赤丸（０）、もう一方は青丸（１）とする必要があります。これが制約です。ところが量子計算機は一般に制約を満たさない解を出力します。たとえば２個の量子ビットの両方が赤丸（０）あるいは両方が青丸（１）となるような解です。このような制約を満たさない解は大きなエネルギー値をもつため、変分法を用いた量子アルゴリズムの精度を悪化させる要因となります。そこで制約適合処理手法を用いることによって、制約を満たさない解を、制約を満たす解に変換することを考えました。すると、制約を満たす解空間において変分パラメタの最適化を行うため、精度高く組合せ最適化問題の最適解を探索することができます。また、本手法は、量子アニーリング計算機、ゲート型量子計算機といった量子計算機のタイプによらず導入することができます。どちらのタイプの実量子計算機においても、本手法が有効であることを明らかにしました。

（３）そのために新しく開発した手法
本手法を用いて制約をもつ組合せ最適化問題を解くことを考えます。この際、制約を満たさないすべての解を、制約を満たす解に変換することのできる制約適合処理手法を構築することがポイントとなります。

今回の研究では、できる限り汎用的な制約適合処理手法を構築することを目指しました。そこで、すべての局所最適解※6が制約を満たす解となるための条件を理論的に証明しました。この条件が満たされるとき、局所最適解を求めるための手法、たとえば貪欲法※7によって制約適合処理手法を構築することができます。この条件は、独立な線形制約※8をもつ組合せ最適化問題に対して成り立ち、現実世界に現れる多くの組合せ最適化問題に対して適用することができます。さらに典型的な組合せ最適化問題に対して、具体的に本手法が適用可能であることを示しました。さらに量子計算機で解くことが困難とされる組合せ最適化問題のグラフ分割問題に対して、制約適合処理手法を組み込んだ場合（提案手法）と組み込まなかった場合とを比較した結果、量子アニーリング計算機では平均して残留エネルギー※9を85%削減、ゲート型量子計算機では平均して残留エネルギーを87%削減し、得られる解の精度が改善することが分かりました（図2）。

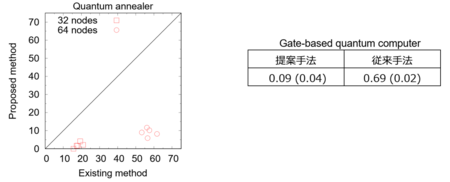
図2. 手法の比較
（左）量子アニーリング計算機を用いて実験を行なった結果を示しています。縦軸横軸は、グラフ分割問題（32頂点および64頂点）を解いたときの残留エネルギーの平均値を表しています（0が最も精度が高い）。縦軸に提案手法、横軸に従来手法を示しました。データが対角線の下側にあることは、提案手法において従来手法より性能が改善していることを示しています。（右）ゲート型量子計算機を用いて実験を行った結果を示しています。グラフ分割問題（4頂点）を解いたときの残留エネルギーの平均値を表しています（カッコ内は平均値の標準偏差を表しています）。

（４）研究の波及効果や社会的影響
本手法を使うことによって、エラーなく実行可能な時間が制限されている量子計算機においても、より精度高く制約をもつ組合せ最適化問題を解くことができます。本手法は量子計算機に簡単に導入することができることから、現在のまたは近未来的に実現する量子計算機の性能を最大限引き出すための量子ソフトウェア開発の要素技術として利用されることが期待されます。たとえば、今回の手法により交通流の最適化が実現すると、渋滞の解消や二酸化炭素排出量の削減など社会的問題へ大きく貢献する可能性があります。

（５）今後の発展
本手法では、制約をもつ組合せ最適化問題を量子計算機で効率的に解く手法を開発しました。今後、一層広範囲な組合せ最適化問題への適用を進めながら、実世界に見られる様々な具体的な問題に対して、本手法の有効性を検証していきます。

（６）研究者のコメント
本研究では量子計算機を精度高く利用するための手法を開発しました。本研究で開発した手法を使うことで、量子計算機の性能が最大限発揮され、今後新たに量子計算機を活用できる事例が増えることを期待します。

（７）用語解説
※1　量子アニーリング計算機
組合せ最適化問題を高速に解決すると期待される計算機。量子効果により量子重ね合わせ状態を実現させ、それを初期状態として用意し、徐々に量子効果を弱める。同時に組合せ最適化問題を表現するイジングモデルの効果を強めることにより、イジングモデルの安定状態を実現させるという機構で動作する。

※2　ゲート型量子計算機
現在の計算機を構成するビットを量子ビットで置き換えた計算機であり、量子ゲートと呼ばれる演算を量子ビットに作用させることで動作する。

※3　組合せ最適化問題
膨大な選択肢の中から､与えられた制約を満たしつつ、関数の最小値（または最大値）をとる選択肢を求める問題の総称。

※4　グラフ分割問題
与えられたグラフの頂点集合を２個の部分集合に分割する問題。それぞれの部分集合に含まれる頂点の個数を等しくするという制約の下、異なる部分集合の間をつなぐ辺の数を最小にする組合せ最適化問題。

※5　変分法
目的関数が最小値（または最大値）となる関数を求める手法。図１では、目的関数がイジングモデルのエネルギー期待値に対応し、変分パラメタの値を更新することでエネルギー期待値の最小値を探索する。イジングモデルのエネルギー期待値の最小値が組合せ最適化問題の最適解の目的関数の値に対応する。

※6　局所最適解
組合せ最適化問題の解のうち、その周囲の解と比較して、局所的に目的関数の値が小さい（または大きい）解。局所最適解は解空間の中にいくつも存在し、その中で目的関数の値を最小（または最大）とする解が真の最適解となる。

※7　貪欲法
組合せ最適化問題に対して、繰り返し、現在得られている解をその周囲の解の中から目的関数の値が最も小さい（または最も大きい）解に更新することで、局所最適解を求める方法。

※8　線形制約
変数が満たす必要のある線形等式や線形不等式のこと。たとえば、図１で一方の量子ビットの値が0、もう一方の量子ビットの値が１という制約は、q_1+q_2=1という線形等式で与えられる（q_i (i∈{1,2})は0もしくは1の値をとる）。

※9　残留エネルギー
組合せ最適化問題を解いた際に得られた解の精度を評価する指標の一つ。得られた解の目的関数の値と真の最適解の目的関数の値の差で与えられ、値が小さいほど解の精度が良いことを表す。

（８）論文情報
雑誌名：IEEE Transactions on Quantum Engineering
論文名：Post-processing variationally scheduled quantum algorithm for constrained combinatorial optimization problems
執筆者名：Tatsuhiko Shirai（早稲田大学）, Nozomu Togawa（早稲田大学）
掲載日：2024年3月13日（水）
掲載URL：https://doi.org/10.1109/TQE.2024.3376721
DOI：10.1109/TQE.2024.3376721

（９）研究助成
研究費名・研究課題名：科学技術振興機構（ＪＳＴ）戦略的創造研究推進事業ＣＲＥＳＴ「地理空間情報を自在に操るイジング計算機の新展開」（JPMJCR19K4）
研究代表者名：戸川望（早稲田大学・教授）
早稲田大学における研究代表者名：理工学術院　教授　戸川望

研究費名・研究課題名：日本学術振興会（ＪＳＰＳ）科学研究費助成事業基盤研究（C）「量子古典ハイブリッド計算技術による物質シミュレーション高速化手法の研究」（21K03391）
研究代表者名：田中宗（慶應義塾大学・准教授）
早稲田大学における研究代表者名：理工学術院　講師　白井達彦